The paper and slides are available. The tail of the slides are a brief
discussion of Tree Set Automata for Prolog Mode Analysis (2016) in hopes of soliciting feedback on the larger
research program.
Abstract:
Rigid Tree Automata (RTAs) are a strict super-class of Regular Tree Automata (TAs), additionally capable of recognizing certain nonlinear patterns such as {f⟨x, x⟩ ∣ x ∈ X}. RTAs were developed for use in tree-automata-based model checking; we hope to use them as part of a static analysis system for a logic programming language. In developing that system, we noted that RTAs are not closed under Kleene-star or pre-concatenation with a regular language. We now introduce a strict super-class of RTA, called Isolating Rigid Tree Automata, which can accept rigid structures with arbitrarily many isolated rigid substructures, such as “lists of equal pairs” by allowing rigidity to be confined within subtrees. This class is Kleene-star and concatenation closed and retains many features of RTAs, including linear-time emptiness testing and NP-complete membership testing. However, it gives up closure under intersection.
BibTeX:
@InProceedings{filardo-eisner-2016-ttatt,
author = {Nathaniel Wesley Filardo and Jason Eisner},
title = {Rigid Tree Automata With Isolation},
booktitle={Proceedings of the Fourth International Workshop on Trends in
Tree Automata and Tree Transducers (TTATT)},
year = {2016},
month = {8},
address = {Seoul}
}
Errata¶
There was a typo in slide 23’s definition of
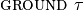 : ⊆ should have been ∈. In fixing this, I have taken the
opportunity to switch to ∈ in all three definitions there.
: ⊆ should have been ∈. In fixing this, I have taken the
opportunity to switch to ∈ in all three definitions there.The slides erroneously claim that TATA’s (G)TSA family cannot recognize singleton subsets of regular languages. This is patently false (in fact, (G)TSA can recognize that a set is of any finite or co-finite cardinality) and I apologize for the error.